Integration by substitution
In calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians. It is the counterpart to the chain rule of differentiation.
Let 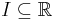 be an interval and
be an interval and ![g�: [a,b] \to I](/2012-wikipedia_en_all_nopic_01_2012/I/dcca1787e4ebe468871937e883ed0c27.png) be a continuously differentiable function. Suppose that
be a continuously differentiable function. Suppose that 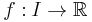 is a continuous function. Then
is a continuous function. Then
Using Leibniz notation: the substitution 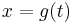 yields
yields 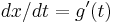 and thus, formally,
and thus, formally, 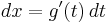 , which is the required substitution for
, which is the required substitution for 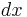 . (One could view the method of integration by substitution as a major justification of Leibniz's notation for integrals and derivatives.)
. (One could view the method of integration by substitution as a major justification of Leibniz's notation for integrals and derivatives.)
The formula is used to transform one integral into another integral that is easier to compute. Thus, the formula can be used from left to right or from right to left in order to simplify a given integral. When used in the former manner, it is sometimes known as u-substitution.
Contents |
Relation to the fundamental theorem of calculus
Integration by substitution can be derived from the fundamental theorem of calculus as follows. Let ƒ and g be two functions satisfying the above hypothesis that ƒ is continuous on I and 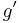 is continuous on the closed interval [a,b]. Then the function
is continuous on the closed interval [a,b]. Then the function 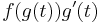 is also continuous on [a,b]. Hence the integrals
is also continuous on [a,b]. Hence the integrals
and
in fact exist, and it remains to show that they are equal.
Since ƒ is continuous, it possesses an antiderivative F. The composite function 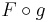 is then defined. Since F and g are differentiable, the chain rule gives
is then defined. Since F and g are differentiable, the chain rule gives
Applying the fundamental theorem of calculus twice gives
which is the substitution rule.
Examples
Consider the integral
If we make the substitution u = x2 + 1, we obtain du = 2x dx and
Here we substituted from right to left. It is important to note that since the lower limit x = 0 was replaced with u = 02 + 1 = 1, and the upper limit x = 2 replaced with u = 22 + 1 = 5, a transformation back into terms of x was unnecessary.
For the integral
the formula needs to be used from left to right: the substitution x = sin(u), dx = cos(u) du is useful, because 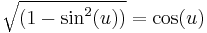 :
:
The resulting integral can be computed using integration by parts or a double angle formula followed by one more substitution. One can also note that the function being integrated is the upper right quarter of a circle with a radius of one, and hence integrating the upper right quarter from zero to one is the geometric equivalent to the area of one quarter of the unit circle, or pi over 4.
Antiderivatives
Substitution can be used to determine antiderivatives. One chooses a relation between x and u, determines the corresponding relation between dx and du by differentiating, and performs the substitutions. An antiderivative for the substituted function can hopefully be determined; the original substitution between u and x is then undone.
Similar to our first example above, we can determine the following antiderivative with this method:
where C is an arbitrary constant of integration.
Note that there were no integral boundaries to transform, but in the last step we had to revert the original substitution u = x2 + 1.
Substitution for multiple variables
One may also use substitution when integrating functions of several variables. Here the substitution function (v1,...,vn) = φ(u1, ..., un ) needs to be one-to-one and continuously differentiable, and the differentials transform as
where det(Dφ)(u1, ..., un ) denotes the determinant of the Jacobian matrix containing the partial derivatives of φ . This formula expresses the fact that the absolute value of the determinant of given vectors equals the volume of the spanned parallelotope.
More precisely, the change of variables formula is stated in the next theorem:
Theorem. Let U be an open set in Rn and φ : U → Rn an injective differentiable function with continuous partial derivatives, the Jacobian of which is nonzero for every x in U. Then for any real-valued, compactly supported, continuous function f, with support contained in φ(U),
The conditions on the theorem can be weakened in various ways. First, the requirement that φ be continuously differentiable can be replaced by the weaker assumption that φ be merely differentiable and have a continuous inverse (Rudin 1987, Theorem 7.26). This is guaranteed to hold if φ is continuously differentiable by the inverse function theorem. Alternatively, the requirement that Det(Dφ)≠0 can be eliminated by applying Sard's theorem (Spivak 1965).
For Lebesgue measurable functions, the theorem can be stated in the following form (Fremlin 2010, Theorem 263D):
Theorem. Let U be a measurable subset of Rn and φ : U → Rn an injective function, and suppose for every x in U there exists φ'(x) in Rn,n such that φ(y) = φ(x) + φ'(x) (y − x) + o(||y − x||) as y → x. Then φ(U) is measurable, and for any real-valued function f defined on φ(U),
in the sense that if either integral exists (or is properly infinite), then so does the other one, and they have the same value.
Another very general version in measure theory is the following (Hewitt & Stromberg 1965, Theorem 20.3):
Theorem. Let X be a locally compact Hausdorff space equipped with a finite Radon measure μ, and let Y be a σ-compact Hausdorff space with a σ-finite Radon measure ρ. Let φ : X → Y be a continuous and absolutely continuous function (where the latter means that ρ(φ(E)) = 0 whenever μ(E) = 0). Then there exists a real-valued Borel measurable function w on X such that for every Lebesgue integrable function f : Y → R, the function (f °φ)w is Lebesgue integrable on X, and
Furthermore, it is possible to write
for some Borel measurable function g on Y.
In geometric measure theory, integration by substitution is used with Lipschitz functions. A bi-Lipschitz function is a Lipschitz function T : U → Rn which is one-to-one, and such that its inverse function T-1 T(U) → U is also Lipschitz. By Rademacher's theorem a bi-Lipschitz mapping is differentiable almost everywhere. In particular, the Jacobian determinant of a bi-Lipschitz mapping det DT is well-defined almost everywhere. The following result then holds:
Theorem. Let U be an open subset of Rn and T : U → Rn be a bi-Lipschitz mapping. Let f : T(U) → R be measurable. Then
in the sense that if either integral exists (or is properly infinite), then so does the other one, and they have the same value.
The above theorem was first proposed by Euler when he developed the notion of double integrals in 1769. Although generalized to triple integrals by Lagrange in 1773, and used by Legendre, Laplace, Gauss, and first generalized to n variables by Mikhail Ostrogradski in 1836, it resisted a fully rigorous formal proof for a surprisingly long time, and was first satisfactorily resolved 125 years later, by Élie Cartan in a series of papers beginning in the mid-1890s (Katz 1982; Ferzola 1994).
Application in probability
Substitution can be used to answer the following important question in probability: given a random variable  with probability density
with probability density 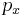 and another random variable
and another random variable  related to
related to  by the equation
by the equation 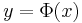 , what is the probability density for
, what is the probability density for  ?
?
It is easiest to answer this question by first answering a slightly different question: what is the probability that  takes a value in some particular subset
takes a value in some particular subset  ? Denote this probability
? Denote this probability 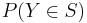 . Of course, if
. Of course, if  has probability density
has probability density 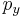 then the answer is
then the answer is
but this isn't really useful because we don't know py; it's what we're trying to find in the first place. We can make progress by considering the problem in the variable  .
.  takes a value in S whenever X takes a value in
takes a value in S whenever X takes a value in 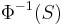 , so
, so
Changing from variable x to y gives
Combining this with our first equation gives
so
In the case where  and
and  depend on several uncorrelated variables, i.e.
depend on several uncorrelated variables, i.e. 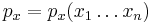 , and
, and 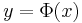 ,
, 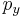 can be found by substitution in several variables discussed above. The result is
can be found by substitution in several variables discussed above. The result is
See also
References
- Hewitt, Edwin; Stromberg, Karl (1965), Real and abstract analysis, Springer-Verlag, ISBN 978-0387045597.
- Ferzola, Anthony P. (1994), "Euler and differentials", The College Mathematics Journal 25 (2): 102–111, doi:10.2307/2687130, http://mathdl.maa.org/mathDL/22/?pa=content&sa=viewDocument&nodeId=2688
- Fremlin, D.H. (2010), Measure Theory, Volume 2, Torres Fremlin, ISBN 978-0953812974.
- Katz, V. (1982), "Change of variables in multiple integrals: Euler to Cartan", Mathematics Magazine 55 (1): 3–11, doi:10.2307/2689856
- Rudin, Walter (1987), Real and complex analysis, McGraw-Hill, ISBN 978-0070542341.
- Spivak, Michael (1965), Calculus on manifolds, Westview Press, ISBN 978-0805390216.
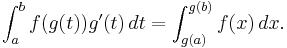
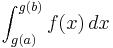
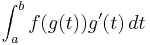
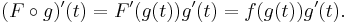
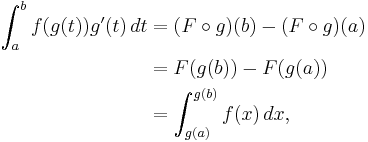
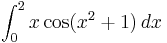
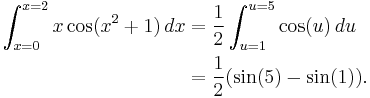
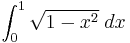
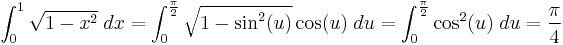
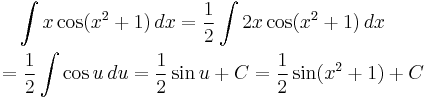
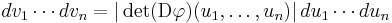
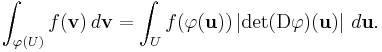
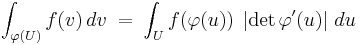
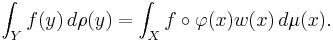
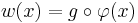
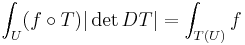
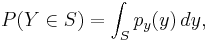
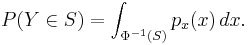
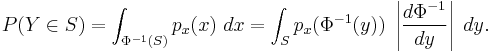
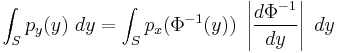
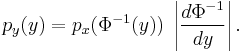
![p_y(y) = p_x(\Phi^{-1}(y)) ~ \left|\det \left[ D\Phi ^{-1}(y) \right] \right|.](/2012-wikipedia_en_all_nopic_01_2012/I/30d20b91eb85078e229bb7603796fff5.png)